Probleme care se rezolvă cu ajutorul ecuațiilor

Ce este o ecuație?

În sens riguros, dar care depășește nivelul matematicii de gimnaziu, o ecuație este un predicat sub forma unei egalități.

La nivel de gimnaziu, ecuația poate fi definită ca o egalitate în care apar una sau mai multe variabile (numite necunoscute) notate cu litere (de obicei $x,y,z$ …).

Exemple:

$2x-7=11 \text{ sau } 9-x=x+3$ – ecuații cu o singură necunoscută

$4x+3y=23$ – ecuație cu două necunoscute

Pentru o ecuație cu o singură necunoscută, soluție a ecuației se numește orice valoare care, pusă în locul necunoscutei, transformă egalitatea într-o propoziție adevărată.

Spunem că $9$ verifică ecuația $2x-7=11$ , deci este soluție a acesteia.

Pentru o ecuație cu două sau mai multe necunoscute, soluție se numește o pereche / triplet etc. de valori care verifică ecuația.

Exemplu: Perechea $(2,5)$ este soluție a ecuației $4x+3y=23$ . Atenție, nu spunem că $2$ și $5$ sunt soluții, ele verifică doar în pereche (nu individual) egalitatea.

A rezolva o ecuație înseamnă a găsi toate soluțiile acesteia, în mulțimea în care ni se cere să le „căutăm”.

În rezolvarea unei ecuații simple cu o singură necunoscută, folosim tehnica „separării” necunoscutei. Aici intervin primele dificultăți pentru un elev de gimnaziu în a face pasul de la „trecem un termen dintr-o parte în alta a egalului cu semn 🙂 schimbat” către proprietățile relației de egalitate.

Să intrăm în lumea proprietăților care ne sunt de ajutor în rezolvarea ecuațiilor.

Proprietăți ale operațiilor cu numere (naturale, întregi, etc.)

$a+b-b=a$
$a-b+b=a$
$a \cdot b:b=a$
$a:b \cdot b=a$
$a:b=c \Leftrightarrow a:c=b$

La proprietățile de mai sus ale operațiilor adăugăm și asociativitatea și comutativitatea adunării și înmulțirii

Proprietăți ale relației de egalitate

1. Dacă $a=b$ atunci:

$a+c=b+c$
$a-c=b-c$
$a \cdot c= b \cdot c$
$a:c=b:c, c \neq 0$

Cu alte cuvinte, dacă într-o egalitate adunăm (scădem / înmulțim / împărțim) și în membrul stâng și în membrul drept același număr, obținem tot o egalitate. De fapt pe aceste proprietăți se bazează așa numita ”trecere dintr-o parte în alta a egalului”. În egalitatea $x+7=12$ , în loc să spunem că îl trecem pe $7$ în dreapta cu „semn schimbat”, de fapt scădem $7$ în ambii membri ai egalității: $x+7=12 \Rightarrow x+7-7=12-7 \Rightarrow x=5$ .

Ca notație uzuală putem folosi $a=b \text{ } \big| +c \Rightarrow a+c=b+c$ . Spunem că „am adunat $c$ în acea egalitate”.

2. Dacă 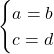$\begin{cases} a=b \\ c=d \end{cases}$ atunci:

$a+c=b+d$
$a-c=b-d$
$a \cdot c=b \cdot d$
$a:c=b:d, c \neq 0$

Din două egalități putem obține altă egalitate adunând (scăzând / înmulțind / împărțind) membrii din stânga, respectiv membrii din dreapta egalului. Spunem că „am adunat (scăzut / înmulțit / împărțit) cele două egalități”.

Exemplu: Să se rezolve în mulțimea numerelor naturale ecuația $3x-1=14$

Soluție: $3x-1=14 \text{ } \big| +1 \Rightarrow 3x=15 \text{ } \big| :3 \Rightarrow x=5$

Două sau mai multe ecuații cu aceleași necunoscute formează un sistem de ecuații. O soluție a unui sistem este o pereche (triplet, etc – în funcție de numărul necunoscutelor) care verifică simultan toate ecuațiile sistemului.

Exemplu: Perechea $(1,3)$ este soluție a sistemului $\begin{cases} 5x-y=2 \\ x+2y=7 \end{cases}$

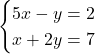
În rezolvarea unui sistem folosim proprietățile de mai sus, împreună cu tehnicile „substituției” sau „reducerii”.

Exemplu: 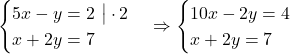$\begin{cases} 5x-y=2 \text{ } \big| \cdot 2 \\ x+2y=7 \end{cases} \Rightarrow \begin{cases} 10x-2y=4 \\ x+2y=7 \end{cases}$ .

Adunând cele două egalități obținem $11x=11 \text{ } \big| :11 \Rightarrow x=1$ .

Înlocuind pe $x$ în prima egalitate, avem $1+2y=7 \text{ } \big| -1 \Rightarrow 2y=6 \text{ } \big| :2 \Rightarrow y=3$ .

Așadar soluția sistemului este perechea 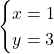$\begin{cases} x=1 \\ y=3 \end{cases}$

Probleme care se rezolvă cu ajutorul ecuațiilor

Un sistem de genul 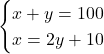$\begin{cases} x+y=100 \\ x=2y+10 \end{cases}$ poate fi „împachetat” într-o „poveste” simplă, care poate suna astfel sub forma unei probleme:

Ionel și Gigel au împreună 100 de lei. Află ce sumă are fiecare știind că Ionel are cu 10 lei mai mult decât dublul sumei lui Gigel.

Problema poate fi rezolvată prin metoda grafică, încă din clasa a IV-a.

Haideți să vedem, în continuare, în ce constă metoda algebrică

PAS 1: Identificarea și notarea (cu litere) a necunoscutelor

PAS 2: „Traducerea”: scrierea ecuațiilor (având necunoscutele notate la pasul 1) care rezultă din datele problemei

PAS 3: Rezolvarea ecuației / sistemului de ecuații (scrise la pasul 2)

CONCLUZII: Scierea în cuvinte a rezultatelor obținute

Iată rezolvarea, însoțită de comentarii, a problemei de mai sus (comentariile cu * nu fac parte din redactarea propriuzisă, ci sunt doar observațiile necesare înțelegerii prin acest exemplu simplu a metodei algebrice)

* Identificăm necunoscutele, în acest caz avem două care coincid cu ceea ce ne cere problema să aflăm (sumele de bani ale celor doi)

Fie $\begin{cases} x \text{ - suma în lei a lui Ionel} \\ y \text{ - suma în lei a lui Gigel} \end{cases}$

* Urmează „traducerea”, avem două informații în textul problemei (ce sumă au împreună și faptul că Ionel are cu 10 lei mai mult decât dublul sumei lui Gigel) pe care le transpunem în două ecuații

$\begin{cases} x+y=100 \\ x=2y+10 \end{cases}$

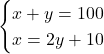
* Din acest moment, lucrăm doar cu ecuații și numere, și proprietățile învățate mai sus. Folosim meotda substituției pentru a rezolva acest sistem, înlocuind pe $x$ în prima ecuație

Avem $2y+10+y=100 \text{ } \big| -10 \Rightarrow 3y=90 \text{ } \big| :3 \Rightarrow y=30$

* Înlocuim acum pe $y$ în oricare dintre cele două egalități inițiale

Rezultă $x=2 \cdot 30+10=70$

* Pentru că problema nu ne-a propus spre rezolvare un sistem, ci ne-a spus o „poveste”, la final e frumos să „traducem” din nou în cuvinte rezultatele obținute

Așadar Ionel are 70 de lei, iar Gigel are 30 de lei.

Acesta este un exemplu clasic și simplu al folosirii metodei algebrice în categoria de probleme care se rezolvă cu ajutorul ecuațiilor”. Mai jos găsiți două fișiere PDF, unul cu probleme rezolvate (diverse tipare, selectate din probleme propuse pentru examenul de Evaluare Națională), iar celălalt cu probleme propuse.

Probleme care se rezolva cu ajutorul ecuatiilor – probleme rezolvate Descarcă

Probleme care se rezolva cu ajutorul ecuatiilor – probleme propuse Descarcă

Spor la mate!

Distribuie