Povestea numărului Pi (𝝅)

Cuadratura cercului și numărul pi. Scurtă biografie a celei mai cunoscute constante matematice

Constanta egală cu raportul dintre lungimea unui cerc și diametrul său

”Începuturile” numărului $\pi$ se pierd undeva în vremuri străvechi când poate vreun iscusit vânător a aflat, probabil din întâmplare, taina minunată a cercului, descoperind numărul $\pi$ , adică raportul dintre lungimea cercului și diametrul acestuia. Pe vremea aceea era asimilat numărului 3. În câmpia Mesopotamiei, a fost, spre exemplu, descoperită o plăcuță de cărămidă arsă pe care scria ”Dacă 60 este lungimea cercului, a treia parte din 60 este 20. Aceasta este diametrul.” Acest raport apare, de a asemenea, în cele mai vechi papirusuri egiptene, în scrierile vechilor hinduși, ale popoarelor din sudul Mexicului, ale chinezilor, dar și în Biblie, unde se consemnează: ”A mai făcut un vas, turnat din aramă, rotund cu totul, de 10 coți de la o margine până la cealaltă și gros cât cuprinde o sfoară lungă de 30 de coți.” Evident, toate aceste scrieri cuprind procedeul practic, intuitiv de construcție și nu o demonstrație a acestor observații.

O problemă mai dificilă decât lungimea cercului și care a preocupat oamenii încă din preistorie a fost aceea a mărimii ariei lui; o problemă ingenioasă deoarece conturul cercului fiind o curbă nu se mai putea încadra în metoda de măsurare a ariilor de tip dreptungi, triunghi, poligon, etc. Sub forma ei ce a pasionat și intrigat numeroase generații de înțelepți, aceea de comparare a ariei unui cerc cu a unui pătrat, este cunoscută drept ”problema cuadraturii cercului”, cea mai renumită problemă de geometrie din toate timpurile, cea care se confundă, practic, cu povestea numărului $\pi$ .

Luată în considerare de geometrii greci, ea a fost considerată deosebită mai ales din perspectiva construirii cu rigla și compasul a unui pătrat de arie egală cu a unui cerc, aspect ce i-a preocupat în mare măsură în special pe pitagoreici începând cu secolul al VI-lea î.e.n., scriind nenumărate lucrări pe marginea acestui subiect. Unele dintre cele mai apreciate sunt cele ale lui Hippocrat din Chios care, încercând să rezolve cuadratura cercului a descoperit mai multe figuri cuadrabile și așa-numitele curbe cuadratice.

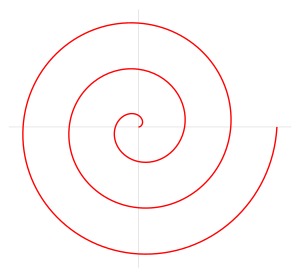
O arhi-cunoscută 🙂 curbă cuadratică este linia helicoidală sau ”spirala lui Arhimede” care descrie o curbă plană determinată de locul geometric al unui punct ce se deplasează cu viteză constantă (plecând dintr-un punct O) pe o dreaptă ce se rotește cu viteză unghiulară constantă în jurul punctului O. Arhimede demonstrează că aria cuprinsă între prima spiră și semidreapta inițială OA este egală cu o treime din aria cercului de rază OA.

Geometrii greci au arătat totuși, fără să demonstreze imposibilitatea cuadraturii cercului cu rigla și compasul, că problema nu se încadrează în așa-zisele probleme ”plane”, ci mai degrabă fizice, lucru dovedit abia in secolul al XIX-lea. Pe lângă încercarea de a găsi soluția problemei cu ajutorul curbelor cuadrice, unii matematicieni greci, precum Antifon, a intuit metoda obținerii ariei cercului (așa cum este cunoscută și azi) prin înscrierea în cerc a unui poligon regulat cu un număr cât mai mare de laturi. Revenind la aproximarea numărului $\pi$ , în scrierea ”Măsurarea cercului” a lui Arhimede este dată o aproximare a raportului dintre lungimea cercului și diametrul său:

$3\cfrac{10}{71}\approx3\cfrac{1}{7}$

Arhimede a avut astfel posibilitatea să determine cu exactitate primele două zecimale ale raportului, aproximând astfel, așa cum este astăzi cunoscut, $\pi=3,14$ . Valoarea determinată de Arhimede a fost folosită de astronomii greci pentru determinarea lungimii razei Pământului. Arhimede, în încercarea sa de a rezolva problema cuadraturii cercului, este singurul geometru din antichitate care a formulat și rezolvat corect problema cuadraturii suprafețelor plane mărginite de linii curbe, fiind, astfel, precursorul calculului integral ce se va dezvolta abia în secolul al XVII-lea, prin lucrările matematicienilor Newton și Leibniz. Deși nu a putut demonstra cuadratura cercului, Arhimede a realizat cuadratura ”segmentului de parabolă”, arătând că aria acestuia este $\cfrac{3}{4}$ din aria triunghiului ce are aceeași bază și aceeași înălțime cu a segmentului de parabolă.

Interesul pentru numărul $\pi$ nu a fost numai al matematicienilor greci. În cea mai veche culegere chinezească, ”Matematica în nouă părți”, prin generalizarea metodei lui Arhimede, considerând un poligon cu 3072 de laturi, s-a ajuns la aproximarea lui $\pi$ cu 5 zecimale exacte, $\pi=3,14159$ . Un alt matematician care a a arătat un interes deosebit asupra numărului $\pi$ a fost persanul al-Biruni (973-1048) care, fără să aibă vreo dovadă precisă, credea că raportul dintre lungimea cercului și diametrul său nu se poate calcula decât aproximativ.

Începând cu dezvoltarea matematicii în Europa (până în secolul XI europenii erau mult în urmă față de orientali în acest domeniu) au existat mulți matematicieni care au crezut în posibilitatea cuadraturii cercului cu rigla și compasul. Printre ei, Jordanus Nemorarius, Campanus din Novara (rămas celebru prin traducerea ”comentată” a ”Elementelor” lui Euclid), Thomas Bradwardinus (poreclit ”doctor profundis”, a susținut cuadratura cercului pe baza ”unghiului de contingență”), sau Albertus de Saxa (primul rector al Universității din Viena).

Deși provenea din zona umanistă, fiind cunoscut ca filosof, Nicolaus din Cusa (1401-1464) a fost cel care a deschis calea aproximărilor cât mai exacte a numărului $\pi$ . Începe o nouă eră în povestea acestui număr: compararea rezultatelor aproximărilor și, cu ajutorul aproximărilor cât mai bune ale lui $\pi$ , rezolvarea problemei cuadraturii cercului în sensul imposibilității ei. Chiar dacă fusese desoperită cu mult timp în urmă de către Arhimede și folosită apoi de matematicienii din Orient, metoda poligoanelor înscrise sau circumscrise unui cerc (cu un număr din ce în ce mai mare de laturi) este cea care aduce la sfârșitul secolului al XVI-lea, 35 de zecimale exacte ale numărului $\pi$ , calcul rezultat din folosirea poligonului cu $2^{61}$ laturi.

În cartea sa ”Vera circuli et hyperbolae quadratura” din 1667, matematicianul englez James Gregory prezintă o demonstrație prin care dovedea imposibilitatea cuadraturii cercului cu rigla și compasul și oferă o nouă metodă de aproximare a numărului $\pi$ , folosind, în locul lungimii arcului de cerc cuprins între laturile poligoanelor regulate înscrise sau circumscrise cercului, aria sectorului de cerc aproximată cu ariile sectoarelor poligoanelor. Ajunge astfel să eludeze metodele geometrice clasice folosite până atunci, prezentându-l pe $\pi$ ca limita unui și convergent de numere (deși noțiunea de limită era foarte vagă la acea dată)

Evident că nu putea rămâne indiferent la chemarea numărului $\pi$ marele matematician Leonhard Euler (1707-1783). El și-a îndreptat atenția asupra șirurilor de poligoane înscrise sau circumscrise cercului care au același perimetru, metodă cunoscută drept metoda izoperimetrelor, demonstrând următoarea teoremă:

Dacă $a_n$ și $b_n$ sunt razele cerucurilor înscrise, respectiv circumscrise unui poligon regulat cu $n$ laturi, iar $a_{2^n}$ și $b_{2^n}$ razele cercurilor înscrise, respectiv circumscrise poligonlui regulat cu $2^n$ laturi, dar de același perimetru $P$ , există relațiile:
$a_{2^n}=\frac{a_n+b_n}{2}, b_{2^n}=\sqrt{\frac{b_n(a_n+b_n)}{2}}=\sqrt{a_{2^n}b_n}$

Trecând la limită se poate deduce valoarea lui $\pi$ . Pornind calculul prin metoda trigonometrică se obține următorul rezultat:

$\frac{2}{\pi}=\lim_{n \to \infty}\cos{\frac{\pi}{4}}\cos{\frac{\pi}{8}}\cos{\frac{\pi}{16}}…\cos{\frac{\pi}{2^{n+2}}}$

Euler mai prezintă în volumul I al cărții ”Opuscula analitica”, două fracții continue care exprimă numărul $\pi$ :

$\frac{\pi}{2}=1+\frac{2}{3+\frac{1\cdot3}{4+\frac{3\cdot5}{4+\frac{5\cdot7}{4+…}}}}$

$\frac{4}{\pi}=1+\frac{2}{7+\frac{1\cdot3}{8+\frac{3\cdot5}{8+\frac{5\cdot7}{8+…}}}}$

Cu puțin timp înainte, demonstrând o teoremă (și reciproca ei) enunțată de T.F. Lagny:

Dacă tangenta trigonometrică a unui arc de cerc este număr irațional, atunci lungimea arcului corespunzător este un număr rațional

un alt mare matematician, J.H. Lambert (1660-1777) reușește să demonstreze riguros faptul că numărul $\pi$ este irațional (plecând de la relația $tg\frac{\pi}{4}=1$ , făcând astfel un pas important spre clarificarea naturii acestuia. Folosindu-se de teoria fracțiilor continue a lui Euler, exprimă și el numărul $\pi$ sub această formă:

$\frac{\pi}{4}=\frac{1}{1+\frac{1^2}{2+\frac{3^2}{2+\frac{5^2}{2+…}}}}$

Această ingenioasă demonstrație a iraționalității numărului $\pi$ a fost reluată în 1794 de către A.M. Legendre (1752-1883), acesta demonstrând și iraționalitatea numărului $\pi^2$ .

Cu toate că se obținuseră încă din secolul al XVIII-lea aceste două rezultate impresionante, problema cuadraturii cercului era încă departe de a fi închisă, putându-se desena mărimi iraționale cu rigla și compasul. Cam în aceeași perioadă, John Machin (1685-1715) a ajuns la calculul cu exactitate a primelor 100 de zecimale ale lui $\pi$ . Pornind de la o serie a lui Gregory și folosind o teoremă a tangentei trigonometrice, a ajuns la următoarea dezvoltare în serie, care a fost folosită de Euler pentru determinarea alteia:

$\frac{\pi}{4}=(\frac{1}{2}-\frac{1}{3\cdot2^3}+\frac{1}{5\cdot2^5}-…)+(\frac{1}{3}-\frac{1}{3\cdot3^3}+\frac{1}{5\cdot3^5}-…)$

cu ajutorul căreia stabilește 128 de zecimale ale lui $\pi$ . Tot el este cel care consacră notația ” $\pi$ ”, introdusă prima oară de W.Jones – reprezentând inițiala cuvântului grecesc ”periphereia”, pentru raportul dintre lungimea cercului și a diametrului acestuia.

Povestea numărului $\pi$ ar fi trebuit să se termine în anul 1882 când Carl Louis Ferdinand Lindemann (1852-1939) demonstrează extrem de riguros că numărul $\pi$ este transcendent și, astfel, este imposibilă cuadratura cercului cu rigla și compasul. El pleacă de la realția lui Euler: $e^{i\pi}+1=0$ , scriind-o sub forma $e^{i\pi}+e^0=0$ și bazându-se pe o ecuație de tip Hermite, demonstrează o altă relație care duce la concluzia clară că numărul $\pi$ nu poare fi irațional algebric, ci transcendent.

Însă bătaia pentru aflarea cât mai multor zecimale exacte ale numărului $\pi$ a continuat cu William Shanks (707 zecimale), dar mai ales o dată cu apariția calculatoarelor. Primul calculator folosit în acest scop a calculat în 1949 primele 2037 de zecimale în aproximativ 70 de ore. Mai târziu, în 1973, milionul de cifre zecimale este depășit.

Formula preferată de programatori pentru a calcula un număr cât mai mare de zecimale cu ajutorul thenologiei avansate se bazează pe o dezvoltare foarte ingenioasă descoperită de Srinivasa Ramanujan la începutul secolului al XX-lea

$\frac{1}{\pi}=\frac{2\sqrt{2}}{9801}\sum_{k=0}^{\infty}\frac{(4k)!(1103+26390k)}{{(k!)^4}396^{4k}}$

O altă formulă de descoperire recentă este formula Bailey–Borwein–Plouffe care permite calcularea în scriere binară sau hexazecimală a oricărei cifre fără a le cunoaște pe cele dinainte:

$\pi=\sum_{k=0}^{\infty}\frac{1}{16^k}(\frac{4}{8k+1}-\frac{2}{8k+4}-\frac{1}{8k+5}-\frac{1}{8k+6})$

Folosind o formulă similară, în anul 2000 s-a stabilit că bitul cu numărul 1.000.000.000.000.000 al lui $\pi$ este 0.

Obsesia pentru acest numâr a dus la inventarea așa-ziselor ”pieme”, poezii ale căror cuvinte, în ordine, au tot atâtea litere cât are cifra cu același numâr de ordine în scrierea lui $\pi$ . Cartea Recordurilor îl menționează în 2005 pe studentul chinez de 24 de ani Lu Chao, care a memorat nu mai puțin de 67.890 de cifre ale faimosului număr. Timpul în care le-a ”recitat” fără greșeală este de 24 de ore și 4 minute. Probabil că această fascinație va continua, existând și astăzi câteva probleme deschise în legătură cu $\pi$ , cea mai cunoscută fiind despre ”normalitatea” acestuia, adică referitor la distribuția uniformă sau nu a cifrelor în scrierea sa, în orice bază de numerație.

De-a lungul timpului, numărul $\pi$ și-a găsit aplicabilitatea în diverse domenii (geometrie, trigonometrie, analiză matematică, numere complexe, integrabilitate, statistică și probabilități, mecanică, fizică, etc.

Și pentru că este un număr care fascinează și în ziua de azi generațiile de elevi, dar mai ales pentru larga sa popularitate, Senatul american a decretat ziua de 14 martie (care în scriere anglo-saxonă a datei este 3/14) drept ziua numărului $\pi$ , zi care este sărbătorită în școli și universități din Statele Unite, dar care se răspândește rapid și în afara tărilor anglo-saxone.

Distribuie

Cuadratura cercului și numărul pi. Scurtă biografie a celei mai cunoscute constante matematice

Lasă un răspuns Anulează răspunsul